С давних времен люди использовали разные способы и методы счета. Они постоянно менялись и совершенствовались, адаптировались к текущим потребностям. Сегодня общепринята во всем мире десятичная система счисления, наряду с ней используются и другие. Самыми востребованными, в основном в программировании, являются двоичная, восьмеричная и шестнадцатеричная. Быстрый перевод разных чисел из одной системы в другую сделает Онлайн конвертер систем счисления.
Первые системы счисления
С тех пор, как между людьми появились торговые отношения, возникла необходимость счета. Первоначально это была единичная система в виде зарубок на палке или камне. Дальше она совершенствовалась и становилась сложнее. Причем устно посчитать было намного проще, чем как-то записать эту информацию. Однако со временем появились знаки, с помощью которых их можно было записать.
Самая примитивная система счисления — единичная. В ней всего один символ. Все последовательные числа образуются его простым повторением.
Главным образом, это была непозиционная система счисления, где каждому числу соответствовал свой символ.
Непозиционная система построена по такому принципу — в ней есть отдельные символы для нескольких чисел, а затем последовательные символы для их кратных. Числа создаются путем добавления дополнительных символов.
Еще в третьем тысячелетии до нашей эры в Египте для обозначения чисел стали использовались иероглифы. Примерно в то же время в Древней Греции для записи чисел использовали буквы своего алфавита. Причем это была первая буква от названия цифры:
| знак | значение | название |
| Ι | 1 | ἴος «иос» |
| Π | 5 | πέντε «пенте» |
| Δ | 10 | δέκα «дека» |
| Η | 100 | ἑκατόν «хекатон» |
| Χ | 1 000 | χίλιοι «хилиой» |
| Μ | 10 000 | μύριοι «мюриой» |
Свои записи чисел были разработаны и в Древнем Риме. Уже тогда Были сформулированы правила для создания новых чисел и проведения с ними разных операций — прибавления, сложения, убавления, деления и т.д. Так появились первые системы счисления.
Система счисления — это способ написания чисел и набор правил, которые позволяют нам выполнять с ними разные математические операции.
Для каждой системы существует набор символов, что используются для записи чисел. Эти знаки — цифры. Их можно складывать различными способами, создавая бесконечное количество комбинаций.
Счет в Древнем Вавилоне
Особого внимания заслуживает достижение ученых Вавилона. Еще четыре тысячи лет назад, они создали первую в мире позиционную систему счисления. Она базировалась на использовании двух значков, где вертикальный клин — 1, а горизонтальный — 10:
Как была построена запись чисел хорошо видно на рисунке.
В шестидесятеричной системе в первый разряд входили числа от одного до шестидесяти — это была основа. 60 единиц из первого разряда образовывали единицу второго разряда, 60 единиц из второго разряда — единицу третьего и т. д. Этот метод счета был разработан на основе шумерской двенадцатеричной системы.
Шестидесятеричная система настолько универсальная и точная, что мы успешно используем ее и сегодня. Ведь именно по ней вавилонские ученые систематизировали время- и летоисчесление. Их год составлял 360 дней, а час 60 минут.
Современные система счисления
Сегодня все мы пользуемся позиционными системы счисления. Их характерными особенностями являются:
- Использование ограниченного количества цифр, которые имеют последовательные значения 0, 1, 2,… Это никоим образом не ограничивает размер записываемых чисел.
- Каждой позиционной системе присваивается определенное значение, которое мы называем базой. Количество цифр равно базовому значению. Для десятичной системы у нас есть набор из 10 цифр, потому что база равна 10. В шестеричной системе цифр будет 6 {0, 1, 2, 3, 4, 5}. В системах с основанием больше 10 нужно больше цифр, чем определено для десятичной системы. Эта проблема решается просто — для записи чисел комбинируют цифры и буквы латинского алфавита. Например, для двенадцатеричной системы берут двенадцать символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. Цифра A равна 10, а цифра B =11.
- Значение цифры в записи зависит от ее положения, отсюда и название « позиционная система». Каждой из них присваивается вес. Он равен последовательным базовым мощностям, отсчитываемым справа.
- Значение числа в обозначении позиции рассчитывается как сумма произведений цифр на веса их позиций.
Десятичная система
Для большинства из нас естественным способом представления чисел является десятичная система. В ней мы учимся считать с детства. Она является основой преподавания математики в школах, ее мы используем в повседневной жизни. Для записи чисел в десятичной системе используют 10 символов: ноль, один, два, три, четыре, пять, шесть, семь, восемь и девять. Они обозначены как: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Отсюда и название.
Десятичное представление счета было создано много веков назад, возможно, потому, что у нас десять пальцев. Эта система позволяет не только просто и рационально представить любое число, независимо от его размера, но и легко выполнять все арифметические операции. Десятичная система является самой распространенной из всех, которые использовались в истории.
Двоичная (бинарная) система
С развитием компьютерных технологий оказалось, что для технических устройств слишком сложно использовать такое большое количество знаков. Это привело к практическому применению систем счета, отличных от десятичной. В информатике первое место занимает двоичная система счисления. Также известная как бинарная, реже ее называют «ноль-один»,
В двоичном счете используют только два цифровых значения «0» и «1». Такой набор является оптимальным для записи любого числа.
Первое число — 0 (ноль), оно не отличается от других систем,
Следующее — 1 (один). В двоичной системе это число тоже существует, оно так и записывается — 1. Дальше по счету идет — 2 (два). Такой цифры при двоичном счете нет, поэтому добавляем еще одну позицию, которая перемещается вправо, она равна нулю. Таким образом, число 2 в десятичной форме имеет записывается, как «10».
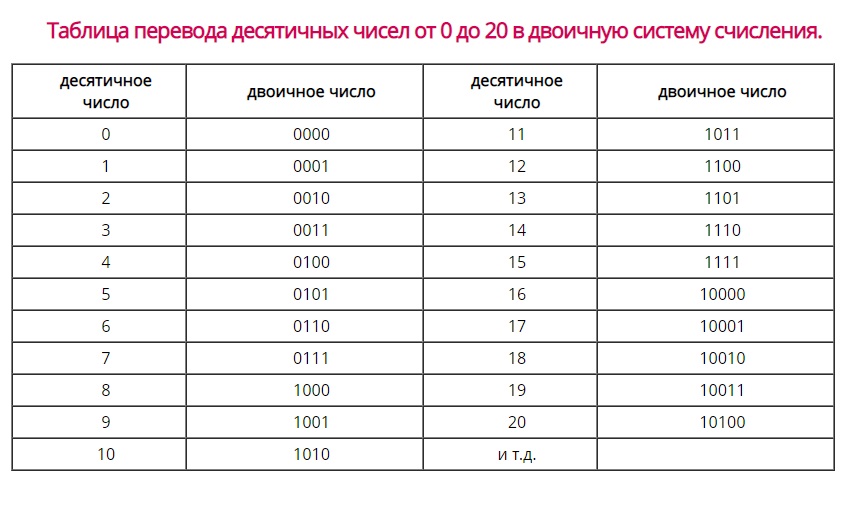
Последующие числа из десятичной системы в двоичной выглядят так:
- 3 — записываем, как «11»,
- 4 — «100»,
- 5 — «101»,
- 6 — «110»,
- 7 — «111»,
- 8 — «1000»,
- 9 — «1001» и т.д.
Принцип все время один и тот же. Двоичный знак (0 или 1) называется битом. Название bit происходит от английского термина Binary Digit. Отсюда и второе название — бинарная система. Хотя в ней присутствуют только 0 и 1, любое число можно записать в двоичном формате. Когда нужен быстрый перевод, чтобы избежать ошибок, используйте конвертер систем счисления.
Алгоритм перевода из десятичной системы в двоичную и наоборот
Перевести числа из двоичной системы в десятичную или из десятичной в двоичную совсем не сложно. Здесь главное понять по какому алгоритму проводить действия. Объясним на примере числа «29», которое мы уже использовали.
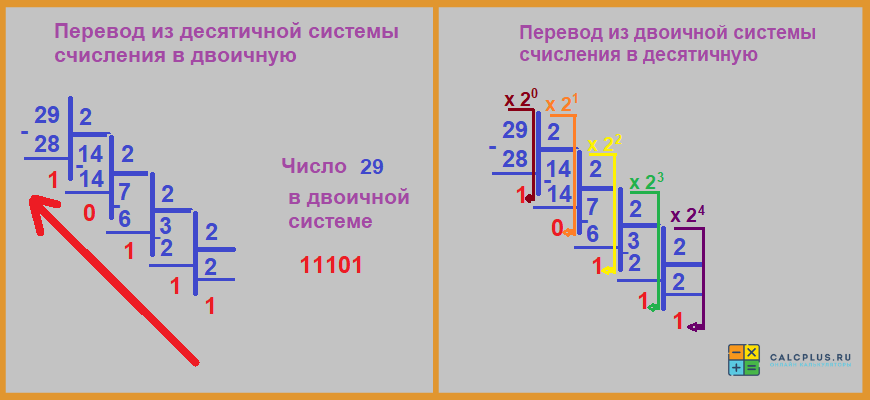
Из десятичной в двоичную
Для такого перевода можно использовать один из двух способов: метод деления на основание (в данном случае 2) или метод подбора степеней (тоже для двойки).
Метод деления визуально более понятный и поэтому используется чаще. Для перевода десятичное число делим обычным способом, «в столбик». на основание.
Для двоичной системы основание число 2, поскольку используем только два символа «0» и «1».
Если в результате деления есть остаток, то ставим «1», если делится без остатка, то ставим «0». Полученное таким образом двоичное число записываем от последнего результата к первому — справа-налево. Как это сделать хорошо видно на рисунке.
Для того чтобы перевести десятичное число в двоичное по методу подбора степеней, необходимо расписать ряд степени двойки и суммировать их. В результате должно получиться исходное число. При этом если степень используем, то ставим «1», если не используем, то «0». Рассмотрим на конкретном примере «29». Распишем степени: 20= 1, 21= 2, 22= 4, 23= 8, 24= 16.
Суммируем от наибольшего значения к наименьшему — 16 + 8 + 4 + 2 + 1
В результате у нас получится 31. Как видим, двойка здесь лишняя, ее мы не используем. Теперь вместо числа, которое мы берем запишем «1», а которое нам не подошло «0».
- 16 это 1;
- 8 это 1;
- 4 это 1;
- 2 это 0;
- 1 это 1
29 в двоичной системе — 11101. Если надо переводить много чисел, используйте конвертер систем счисления.
Чтобы упростить возведение двойки в степень, мы сделали для вас таблицу.
Из двоичной в десятичную
Берем двоичное число 11101. Расписываем сумму степеней. Так как у нас 5 символов, то самая большая степень это 24, поскольку есть нулевая. Умножаем каждую цифру двоичного числа на соответствующую степень (см. рисунок).
1×24 + 1×23 + 1×22 + 0×21 + 1×20 = 16 + 8 + 4 + 0 + 1 = 29
Для удобства приведем таблицу, но проще использовать конвертер систем счисления.
Восьмеричная система
В восьмеричной системе используют восемь цифр: 0, 1, 2, 3, 4, 5, 6 и 7 — отсюда и название. Она также позиционная и работает по тому же принципу, что и десятичная. Это означает, что когда цифра достигает своего максимального значения, то дальнейший счет идет путем увеличения позиции.
Объясним на примере. Давайте преобразуем последовательные числа и посмотрим, в чем разница.
- Число ноль (0) одинаково в обеих системах.
- То же самое и для единицы (1), двойки (2), тройки (3) и т.д. вплоть до семи (7).
Дальше ситуация усложняется, на очереди еще один номер — восемь. Восьмеричная система не знает такой цифры. Здесь срабатывает такой же принцип, как для двойки в двоичной. Таким образом,
число восемь «8» по десятичной системе в восьмеричной будет записано «10»,
- «9» — как «11»,
- «10» — как 12,
- «11» — как «13»,
- «12» — как «14» и т.д.
Это легко проверить, используя метод позиционирования. Составляем уравнение для «14» по восьмеричной —
1 × 8 + 4 × 1 = 8+4 = 12 по десятичной.
Как переводить из десятичной системы в восьмеричную и шестнадцатеричную хорошо видно на рисунке.
Быстро и без ошибок с таким переводом справится наш конвертер систем счисления.
Шестнадцатеричная система
Позиционная система, в которой для записи чисел используются цифры и буквы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. От других систем она отличается самой короткой записью чисел. Таким значением легче манипулировать, и он потребляет меньше памяти. Например, число
- «12» в десятеричной,
- «1100» в двоичной,
- «14» в восьмеричной,
- «С» в шестнадцатеричной.
В информатике шестнадцатеричная система используется, например, для адресации ячеек памяти устройствами или для кодирования цветов, используемых на веб-сайтах.
Как следует из названия, в основе этой системы лежит число 16. Поскольку она позиционная, то в обозначении числа каждая позиция имеет значение в шестнадцать раз больше, чем предыдущая. По логике чисел должно быть шестнадцать. Первые десять, как обычно — 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Дальше для односимвольной маркировки используют буквы алфавита:
- 10 — А,
- 11 — В,
- 12 — С,
- 13 — D,
- 14 — E,
- 15 — F.
«16», по той же логике, что и в предидущих системах у нас будет «10».
Принято, что если в начале числа есть буква, перед ней следует ставить ноль, здесь он не имеет никакого значения — это является чисто формальным.
Чтобы избежать путаницы при записи числового ряда, принято писать «h» после каждого шестнадцатеричного числа. Последовательность будет выглядеть так:
0h, 1h, 2h, 3h, 4h, 5h, 6h, 7h, 8h, 9h, 0Ah, 0Bh, 0Ch, 0Dh, 0Eh, 0Fh, 10h, 11h, 12h, 13h, 14h, 15h, 16h, 17h, 18h, 19h, 1Ah, 1Bh, 1Ch, 1Dh, 1Eh, 1Fh, 20h, 21h, 22h, и т.д., что почти похоже на десятичную систему, за исключением того, что есть еще шесть цифр. Также важен способ произношения шестнадцатеричных чисел. Например, число 212h читается не «двести двенадцать», а «два-один-два» и соответствует 530 в десятичном счете.
Кроме этих основных используются и многие другие системы счисления — троичная, четверичная, пятеричная, семеричная и т.д. Какие символы для записи чисел используются для них указано в таблице.
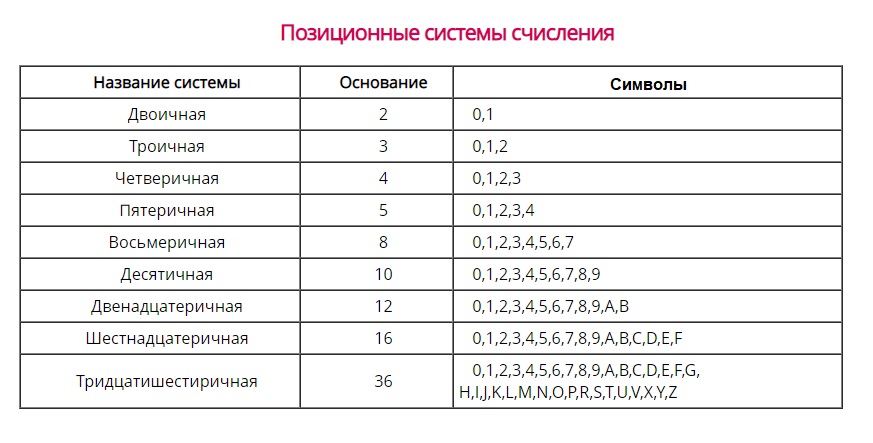Быстро конвертировать из одной в другую вы можете используя конвертер систем счисления.
Как переводить двоичные числа в другие системы счисления вы узнаете из видео
Читайте далее:
